Leading into the final weekend of the season, the only thing that has been decided is that Wisconsin will finish last and Ohio State next to last. All four top spots are still up for grabs with each team having the potential to finish anywhere from first to fourth. There are four games of consequence. Penn State travels to Minnesota for two games while Michigan and Michigan state will have a home and home series.

The most likely scenario, of course, would be for all four games to be won by the home team. Should that happen, Minnesota would win the regular season championship, with Michigan State second, Michigan third, and Penn State fourth.

The least likely scenario, would be for the visiting teams to win each game. Should that happen, then Penn State is the champ, Michigan State takes second, Michigan third, and Minnesota fourth.

Note: the above assumes that none of the games go to a shootout. More on that later.

At first, it might seem like a simple task to figure out the tournament picture. After all, the Big Ten Conference has a shoot-out rule so a winner is determined for every game. Four games, each with only two possible outcomes. My math studies say that’s 16 distinct outcomes. But since Team A winning the first and losing the second is the same as losing the first and winning the second, we really only have nine different scenarios. Nine different outcomes is certainly manageable.

Not so fast. Under the Big Ten’s shootout rule, the game is official considered a tie with each team earning a point and the shootout winner earning a second point (a normal winner, i.e. in regulation or overtime, earns three points).

That adds a whole new level of complexity to the matter. In fact, it means that there are now 49 possible outcomes to the four games this weekend. I’m not going to map out all 49 scenarios.  (NOTE:  Some later mathematical gymnastics made me realize there are even more than 49 scenarios – I’m not going to waste time trying to figure out how many more).

But what I will try to do is figure the subset of those that affect Penn State in the tournament, particularly those that will earn PSU a bye on Thursday. The tournament is a six team single elimination affair with the top two seeds earning byes for the Thursday opening round. The third seed faces the sixth seed with the winner advancing to meet the second seed on Friday. The fourth seed faces the fifth with the winner moving on to get the top seed on Friday.

Seeding for the tournament is done by points earned during conference play. If two teams have the same point total, the tie is broken by total wins not by head-to-head results. This distinction could become very important in some of our scenarios.

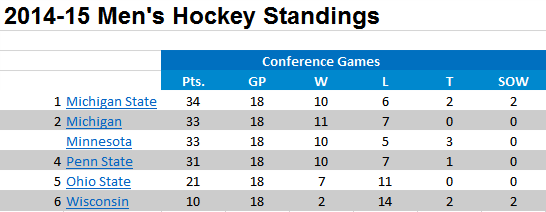
Current standings look like this.

From here, I’ll breakdown the results from Penn State’s perspective, starting out with those that are most favorable to us. Initially, I will not include any possible shootouts between Penn State and Minnesota but will follow up later on those.

So here we go:

Penn State sweeps Minnesota.

Maybe the most important thing to know is that, in a way, we control our destiny. If we win both games in Minnesota, we will get a bye for the opening round. Whether that’s a first or second seed bye would be determined by the out come of the Michigan/MSU games.

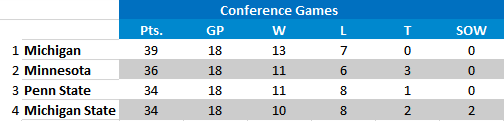
As mentioned above, if PSU sweeps and Michigan and MSU split, we would be the champs and get the first seed. The standings would look like this.

We would own the tiebreaker by virtue of having more Big Ten wins than MSU despite the fact that they have a better head-to-head record with us.

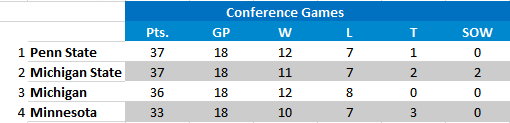
If Michigan were to sweep Michigan State, then we would drop to second but would still have a Thursday bye. Those standings would be:

Similarly, if Michigan State were to sweep, they would swap places with MSU. We would still be second and still have the bye. Those standings would be:

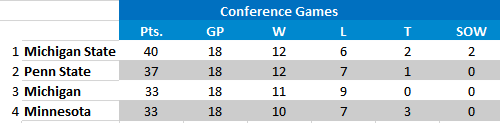
Note in this case, Michigan would be a three seed over Minnesota by virtue of having more conference wins.

Obviously, a sweep is good for us since it locks us into a bye.

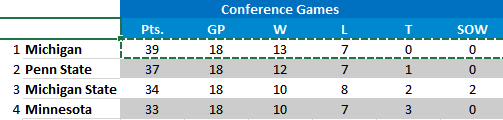
Note: There is also one scenario where shootouts in the Michigan/Michigan State series would affect us. That would be if Michigan sweeps MSU but wins both of their games via a shootout. In that unlikely case, we would actually get the first seed over Michigan. The standings would look like this:

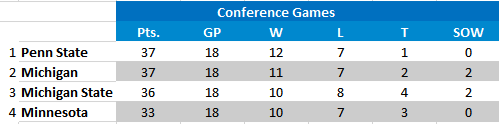
In this case we would own the tiebreaker over Michigan due to more conference wins.

The other Michigan/MSU shootout scenarios all still leave us in second.

Minnesota sweeps Penn State.

This is the simplest scenario of all. If the Gophers take two from us, we wind up in fourth place and will face Ohio State on Thursday of the Big Ten tournament. Since I’m only really interested in where we finish, I’m not going to bother drawing up all the possible scenarios.

Penn State and Minnesota split

In most cases, if we split with Minnesota we will wind up fourth. There is one case, however, where we do wind up third. That would be if we split and Michigan sweeps MSU. In that case the standings would look like this:

We would own the tiebreaker over MSU by virtue of our more conference wins. The only difference it would make would be that we would face Wisconsin in the opening round on Thursday rather than Ohio State. Of course, given how poorly we’ve played against Ohio State as compared to Wisconsin, this might be considered a pretty big difference.

What I haven’t yet covered is any scenarios that involve either or both of the Penn State/Minnesota games ending in a shootout. I’ll go through those scenarios tomorrow (assuming that the Big Ten offices don’t have their computers churn through the possibilities and publish them – if they do, you can simply count on a link from me).

 

NOTE:  I just realized that I forgot to update the games played column in each of the charts.  They should each read 20 games but I’m not going to take the trouble to go back and redo all of them since it doesn’t affect any of the calculations.